🔗What is FizzBuzz?

From Wikipedia:

FizzBuzz is a group word game for children to teach them about division. Players take turns to count incrementally, replacing any number divisible by three with the word "fizz", and any number divisible by five with the word "buzz", and any number divisible by both 3 and 5 with the word "fizzbuzz".

This simple game can easily be turned into a programming interview question as follows:

For an integer i, $1 \leq i \leq 100$, print:

• "Fizz" if i is divisible by 3.
• "Buzz" if i is divisible by 5.
• "Fizz Buzz" if i is divisible by 3 and 5.
• i (the number itself) if none of the above conditions are true.

Any CS graduate is bound to get asked to code FizzBuzz at some point. So let's see the first answer to this problem:

🔗Straightforward implementation

int main() {
  for (int i=1; i<=100; i++) {
     if (i % 3 == 0 && i % 5 == 0) {
       printf("Fizz Buzz\n");
     }
     else if (i % 5 == 0) {
       printf("Buzz\n");
     }
     else if (i % 3 == 0) {
       printf("Fizz\n");
     }
     else {
       printf("%d\n", i);
     }
  }
}

🔗Explanation:

We use the modulo operator % (present in all well-known programming languages) to test whether $i$ is a multiple of the numbers 3 or 5 or both. Then, based on these tests, we branch out and print out Fizz or Buzz or FizzBuzz or the number itself.

Can we do better though? Is there some way to optimize this code and perhaps use fewer tests?

Well, Bob comes along, and says that he has a simpler (more optimized) solution to FizzBuzz. He is kind enough to share his code with us. Let's take a look:

🔗Bob's implementation

int main() {
  for (int i=1; i<=100; i++) {
     if (i % 15 == 0) {
       printf("Fizz Buzz\n");
     }
     else if (i % 5 == 0) {
       printf("Buzz\n");
     }
     else if (i % 3 == 0) {
       printf("Fizz\n");
     }
     else {
       printf("%d\n", i);
     }
  }
}

Bob claims that we can condense the first test i.e. checking whether $i$ is divisible by both 3 and 5 to just checking whether $i$ is divisible by 15, thereby reducing the test cases from four to three.

Running our implementation and Bob's, we see that we get the exact same output. Why does this work?

🔗Some math

Checking whether the remainder of $i$ divided by a number $x$ is equal to 0 is equivalent to :

$$ i \equiv 0 \quad \text{(mod x)} $$

That is, we are testing a Congruence relation under the hood.

In the FizzBuzz coding task we are testing the following congruence relations:

$$ i \equiv 0 \quad \text{(mod 3)} $$

$$ i \equiv 0 \quad \text{(mod 5)} $$

If both of the relations are satisfied i.e. $i$ is divisible by both $3$ and $5$ then we print "Fizz Buzz". Mathematically, this translates to finding a unique solution to the previous system of congruences. How do we do that?

🔗Chinese Remainder Theorem (CRT)

Specifically the unique solution modulo N is found by:

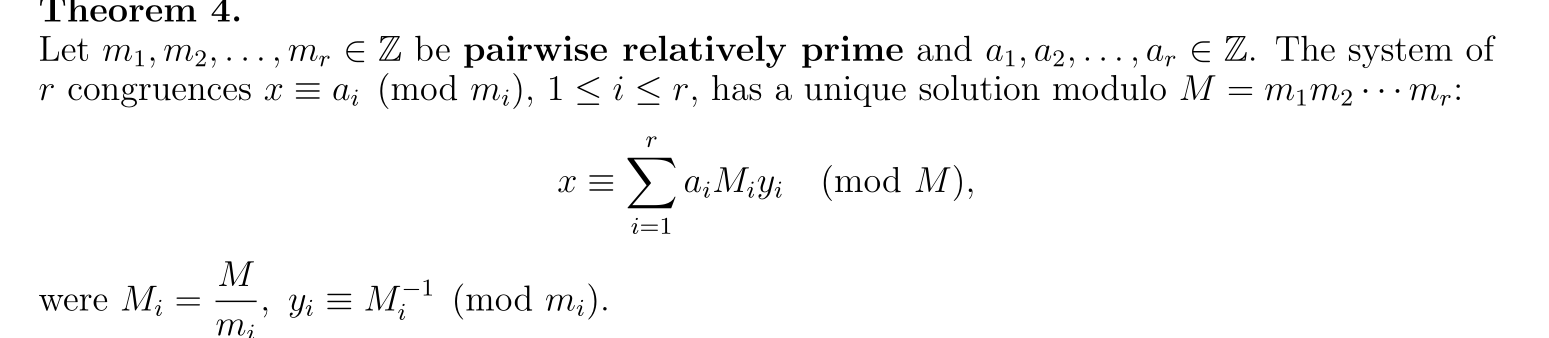
🔗Applying CRT to FizzBuzz

In our case, $m_1 = 3$ and $m_2 = 5$.

$$ gcd(m_1, m_2) = gcd(3, 5) = 1 $$

Hence, 3 and 5 are coprime and we can apply the Chinese Remainder Theorem.

$ M = m_1 \times m_2 = 3 \times 5 = 15$

We need not calculate the multiplicative inverses $y_1$, $y_2$ nor the coefficients $M_1$, $M_2$ since $a_1 = a_2 = 0$

Therefore, CRT gives us the following solution:

$$ i \equiv 0 \quad \text{(mod 15)} $$

🔗What have we just proved?

We have proved the following statement:

If an integer $i$ is divisible by both $3$ and $5$, then it is divisible by $15$.

Generally for two co-prime integers $a, b$ :

$$ lcm(a, b) = a \times b $$ where $lcm$ = least common multiple. This is because for any integers $j$, $k$, $gcd(j,k) \times lcm(j,k) = j \times k$. If j,k are co-prime, $gcd(j,k) = 1$.

This implies that:

integer $i$ is divisible by both $a$ and $b$ if and only if $i$ is a multiple of $ab$.

We have finally validated Bob's implementation and explained a simpler solution to FizzBuzz, one that is not immediately clear to the naked eye as to why it works :)